Чому не можна поділяти світ на «фізиків» і «ліриків»

Один із аргументів проти обов’язкового ЗНО з математики — нібито є «математичний» склад мислення, а є — «гуманітарний». Перший — аналітичний, тоді як другий включає творчі здібності, гнучкість та креативність. І ця природна особливість начебто робить нас нерівними перед тестуванням. Таке «бінарне» розмежування вкоренилося в нашій свідомості. Ми точно знаємо, до котрого з «таборів» належимо, й боїмося, що, зайшовши на «чужу» територію, напевно зазнаємо невдачі.

І ми майже не усвідомлюємо, що цей стереотип — не просто хибний, а ще й деструктивний. Коли хтось називає себе гуманітарієм (а це зовсім не означає наявність у людини докторського ступеня з філології), то, дуже ймовірно, математика з фізикою йому «не зайшли» й він навісив на себе такий ярлик.

Можна припустити, що «математична травма» почалася з нудного уроку, незацікавленості предметом або конфлікту з учителем. А можливо, вчитель був хороший, але на уроках орієнтувався на розвиток «зірок» і не брав до уваги, що матеріал для когось був заскладним. Ну, а потім, як наслідок, — перша «дурна» задача, якої не вдалося розв’язати зразу, бо забракнуло певних знань. Хто винен? Учитель, який не зацікавив? Батьки, які вчасно не зреагували й не допомогли? Чи Міністерство освіти? Персоналізована відповідальність потребує дій, а ось безособовий ярлик «гуманітарний склад мислення» перекладає відповідальність на безмовну природу, і цим усе кінчається. Але, поділяючи на світ на «фізиків» і «ліриків», ми обмежуємо власні можливості. Досить повторити кілька разів, що учень — гуманітарій, і дитина зневірюється у своїх аналітичних здібностях. Учні ж із ярликом «технар» підсвідомо закреслюють для себе реалізацію у творчості, вивченні іноземних мов та в багатьох інших гуманітарних галузях.

Дослідження останніх років дедалі більше схиляються до висновку, що математичного і нематематичного способів мислення не існує.

Британський математик, професор Оксфордського університету і відомий популяризатор науки Маркус дю Сотой упевнений, що ми всі — «математики». Так, окремим людям може нелегко даватися арифметика (приблизно 5% популяції — це люди, яким властивий математичний аналог дислексії — дискалькулія), але виявлення шаблонів, розпізнавання симетрій і відчуття форм — набагато важливіші навички для вивчення математики: саме вони сформувалися в результаті еволюції і мають велике значення для виживання популяції. Наприклад, розпізнавання симетрії потрібне для прийняття швидких рішень, коли людина бачила симетричні патерни в живій природі: скажімо, симетричні морди тварин. Можна було або з'їсти тварину і вижити, або ж навпаки, бути з’їденим твариною. Так само люди з розвиненим відчуттям чисел могли оцінити, чи перевершують вороги їхнє плем'я кількісно — і на підставі цього вирішити: битися чи рятуватися втечею.

Усвідомивши, що всі ми «математики», можна впевнитися і в тому, що математика й творчість — міцно переплетені. Справді, під час уроків із математики учні розпізнають закономірності й симетрії, вчаться працювати з формами, пропорціями, оцінювати розміри, розвивають просторове мислення... А це ж і про красу! Схожими речами ми займаємося, коли малюємо, граємо на музичних інструментах, ліпимо. Отже, такі навчальні дисципліни як математика і мистецтво перетинаються і спрямовані на розвиток схожих навичок.

Як у математиці, так і в мистецтві є підготовча частина: робота над шаблонними вправами, арифметика, квадратні рівняння, змішування фарб, підготовка полотна, нудні години сольфеджіо. Все перелічене не є мистецтвом, це — лише підготовка до акту творчості. Сам акт — створення художніх або музичних шедеврів чи розв’язання математичних задач (як шкільних, так і відкритих наукових), під час якого важливі й отриманий результат, й естетичне задоволення від краси «елегантного» розв’язку.

Бертран Рассел називав красу математики суворою, а ось відомий математик Чарльз Ла́твідж До́джсон (Льюїс Керрол) у своїх творах продемонстрував світові математичну красу через фантазії, легку гру слів та математичну логіку.

З часів античності у піфагорійців музика і гармонія були першим доказом на користь того, що космічні явища можна описати математично. Вважалося, що схоже гармонійне розташування планет теж породжує «музику сфер». Відомий англійський математик Ґодфрі Гарольд Гарді сказав: «У математика, як і в поета, й живописця мають виходити красиві візерунки». А створення красивих візерунків — є однією з математичних задач. Ось вам приклади.

Один із незвичайних математичних об’єктів (прототип фракталу), який із ХІХ ст. носить назву «множина Кантора», був відомий ще людям у Стародавньому Єгипті: цим зображенням прикрашали колони, а самоподібні фрактальні структури властиві орнаментам африканських племен і використовувалися під час планування поселень (рис. 1).

 Рис. 1 Фрактали в культурі. (1) — множина Кантора на колоні у Стародавньому Єгипті, (2) — план африканських поселень, (3) африканська маска з елементами трикутників Серпінського ( з книги Ron Eglash African Fractals).

Ще один із маловідомих прикладів математики в мистецтві — явище храмової геометрії в Японії. Виявом цієї традиції є дерев'яні таблички сангаку (рис.2), на яких викарбовували або малювали математичні задачі. Вони зробили величезний внесок у розвиток математики в Японії. Геометричні теореми замість образів святих з'являлися під дахами в синтоїстських храмах як виклик усім охочим знайти елегантний розв’язок, красу і натхнення.

Рис. 2. Дерев'яні японські таблички сангаку, на яких викарбовували або малювали математичні задачі

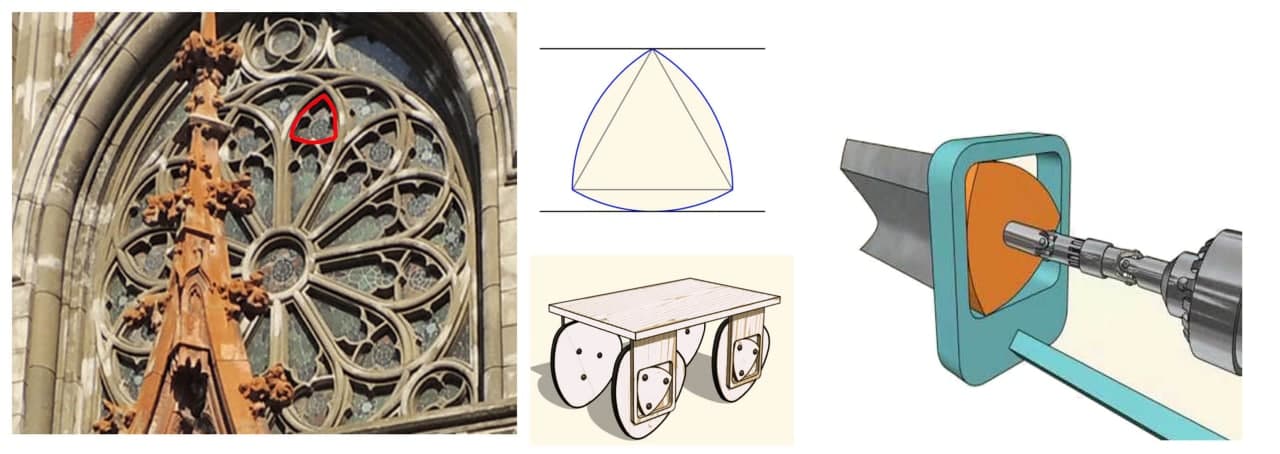
 Якщо повернутися до середньовічної Європи, то тут математичні знання втілилися в характерних візерунках готичних віконних отворів, які демонструють складні геометричні конфігурації, створені поєднанням основних геометричних фігур — кіл та прямих ліній. Щоб надихнутися всеосяжністю математики в готичних формах, не треба далеко їхати, досить придивитися до фасаду київського костелу Святого Миколая. Тут, окрім вписаних кіл, можемо побачити важливу в інженерній науці фігуру — трикутник Рело, що є простішою після кола фігурою постійної ширини.

Від казкового палацу Альгамбра в Гранаді до п’ятничної мечеті в Ісфагані (Іран) — краса й математичний спадок проявляються в ісламських геометричних малюнках, які майже всюди можна бачити в мечетях, медресе та палацах. Візерунки ряхтять на будівлях, кераміці, монетах, гобеленах і картинах, що демонструє величезне розмаїття математичних навичок, необхідних майстрам, які їх створювали. 

Рис. 4. Паркети математика. (1) — «Ящірки» Ешера, (2) — мозаїка з палацу Альгамбри, (2) — паркет Пенроуза. 

Саме арабські мозаїки дарували найбільше натхнення художникові Моріцу Ешеру, який у своїх роботах використовував базові елементи, побудовані на трикутниках, квадратах і шестикутниках (рис. 4). Він перевтілив ці фігури у тварин, птахів, рептилій. Такі спотворені основи мозаїк зберігали властивість замощення площини без перекриттів і щілин. Сам Ешер казав, що «в школі був дуже поганим учнем», і дивувався, що математики використовують його малюнки для ілюстрації своїх книжок. Фантазії Ешера зараз допомагають учителям у поясненні таких математичні понять як: паралельне перенесення, подібність фігур, рівновеликі фігури, періодичність, квазіперіодичність, замощення площини. Із допомогою анаморфного мистецтва (коли картину або скульптуру можна побачити тільки з певної точки чи з допомогою спеціальних предметів, наприклад конічних або циліндричних дзеркал) у роботах угорського митця Іштвана Ороса чи скульптора Джонті Хартвіца можна унаочнювати і пояснювати школярам різні відображення площини або простору на себе.

Вчитель математики, який любить свій предмет, може знайти математичні патерни, закономірності й задачі у світі мистецтва і захопити математикою дітей, які, можливо, позіхали, розв’язуючи логарифмічні нерівності. Саме тому дуже актуальним в освіті STEAM стає підхід, який включає ще один важливий компонент — Art. Завдяки інтеграції мистецтва, математики та природничих наук можна зробити заняття цікавими для більшості учнів. Сприймаючи інтегровані мистецтво й математику, школярі навчаються розширювати усвідомлення того, ким вони є насправді: і математиками, і митцями!

Ще один зі співзвучних сучасних трендів освіти — музейна педагогіка, яка базується на міждисциплінарному підході в умовах музейного середовища. Такі уроки зі STEАM у музеї стають зараз популярними в нашому київському Національному музеї мистецтв імені Богдана та Варвари Ханенків. На один із них — для юних митців і математиків — «Коло та його властивості на матеріалі творів з колекції Музею Ханенків», створений спільно з НЦ МАН України, я вас і запрошую.